

우아한형제 기술블로그를 보던 중, 이목을 끄는 제목을 발견하고 글을 읽게 되었습니다.
고르곤졸라는 되지만 고르곤 졸라는 안 돼! 배달의민족에서 금칙어를 관리하는 방법 | 우아한형
안녕하세요! 셀러시스템팀에서 서버 개발을 하고 있는 김예빈이라고 합니다. 배달의민족에는 금칙어를 관리하는 "통합금칙어시스템"이라는 것이 있습니다. 금칙어란? 법 혹은 규칙으로 사용이
techblog.woowahan.com
블로그를 통해 아호코라식 알고리즘에 대해 알게 되었습니다.
아호코라식 알고리즘은 일대다 패턴 매칭 알고리즘으로, 개선의 여지가 없을 정도로 완벽한 성능을 자랑한다고 알려져 있습니다.
아호코라식 알고리즘을 공부하기에 앞서, 문자열 매칭 알고리즘인 KMP 알고리즘에 대해 먼저 학습하면, 나중에 아호코라식 알고리즘을 이해하는데 도움이 될 것 같아 KMP 알고리즘을 공부하기로 했습니다.
서론

문자열 'ABACABAACABACABBC'에서 패턴 'ABACABAC'를 찾는 방법은 여러 가지가 있습니다.
가장 간단한 방법은 Brute-force 알고리즘을 사용하여 index 값을 1씩 증가시키며 패턴의 일치 여부를 확인하는 것입니다.
하지만 이 방법은 문자열의 길이를 N, 패턴의 길이를 M으로 할 때, 시간 복잡도가 O(MN)으로 비효율적입니다.
반면, KMP 알고리즘을 사용하면 이 시간을 효과적으로 줄일 수 있습니다.
KMP 알고리즘이란?
KMP(Knuth-Morris-Pratt) 알고리즘은 시간 복잡도가 O(N + M)인 문자열 내에서 특정 패턴을 찾아내는 문자열 검색 알고리즘입니다.
KMP 알고리즘역시 패턴을 문자열에서 좌에서 우로 비교하는 방식은 동일하지만, Brute-force 알고리즘과의 차이점은 위치를 더 효율적으로 이동시킨다는 점입니다. 문자열 검색 시 불필요한 문자 간 비교를 피하기 위해 먼저 실패 함수(Failure Function)을 구해야 합니다.
실패함수
실패 함수는 탐색 문자열의 부분 중에서 접두사이면서 접미사인 최대 문자열을 구하여 배열 형태로 저장하는 역할을 합니다.
예를 들어, 패턴이 'ABCDABD'라고 가정하면, 실패 함수를 실행했을 때의 배열 F의 결과는 다음과 같습니다.
| 인덱스(i) | 패턴 문자열 | 접두사 = 접미사 | F(i) |
| 0 | A | 없음 | 0 |
| 1 | AB | 없음 | 0 |
| 2 | ABC | 없음 | 0 |
| 3 | ABCD | 없음 | 0 |
| 4 | ABCDA | A | 1 |
| 5 | ABCDAB | AB | 2 |
| 6 | ABCDABD | 없음 | 0 |
배열 F를 구하는 코드는 다음과 같습니다.
static void failureFunction(String pattern) {
F = new int[pattern.length()];
for (int i = 1, j = 0; i < pattern.length(); i++) {
while (j > 0 && pattern.charAt(i) != pattern.charAt(j)) {
j = F[j - 1];
}
if (pattern.charAt(i) == pattern.charAt(j)) {
F[i] = ++j;
}
}
}
KMP 알고리즘
문자열이 'ABCDABCDABDE'이고, 패턴이 'ABCDABD'라고 가정하겠습니다.
과정은 다음과 같습니다.
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 문자열 | A | B | C | D | A | B | C | D | A | B | D | E |
| 패턴 | A | B | C | D | A | B | D |
문자열과 패턴을 비교했을 때, 마지막 D에서 불일치가 발생했습니다.
이는 6번째 인덱스에서 불일치가 발생한 경우입니다. 이 경우 5번 인덱스까지는 일치했음을 의미합니다.
이때, 위에서 구한 F함수에서 F[5] = 2이므로, 2번째 인덱스인 C부터 다시 비교하면 됩니다.
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 문자열 | A | B | C | D | A | B | C | D | A | B | D | E |
| 패턴 | A | B | C | D | A | B | D |
이를 코드로 구현아면 다음과 같습니다.
static int KMP(String text, String pattern) {
for (int i = 0, j = 0; i < text.length(); i++) {
while (j > 0 && text.charAt(i) != pattern.charAt(j)) {
j = F[j - 1];
}
if (text.charAt(i) == pattern.charAt(j)) {
if (j == pattern.length() - 1) {
return i - j;
} else {
++j;
}
}
}
return -1;
}
전체 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
static int[] F;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
String T = br.readLine();
String P = br.readLine();
failureFunction(P);
System.out.println(KMP(T, P));
br.close();
}
static int KMP(String text, String pattern) {
for (int i = 0, j = 0; i < text.length(); i++) {
while (j > 0 && text.charAt(i) != pattern.charAt(j)) {
j = F[j - 1];
}
if (text.charAt(i) == pattern.charAt(j)) {
if (j == pattern.length() - 1) {
return i - j;
} else {
++j;
}
}
}
return -1;
}
static void failureFunction(String pattern) {
F = new int[pattern.length()];
for (int i = 1, j = 0; i < pattern.length(); i++) {
while (j > 0 && pattern.charAt(i) != pattern.charAt(j)) {
j = F[j - 1];
}
if (pattern.charAt(i) == pattern.charAt(j)) {
F[i] = ++j;
}
}
}
}
코드를 통해 4번째 인덱스부터 일치함을 확인할 수 있습니다.
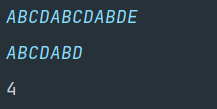
추가적으로, 위의 코드를 응용하여 아래 문제를 풀어보시면 좋을 것 같습니다.
https://www.acmicpc.net/problem/1786
참고자료
[알고리즘] KMP 알고리즘
개발을 기록하는 블로그 '[알고리즘] KMP 알고리즘'을 한 번 살펴보세요.
baeharam.github.io
'Algorithm' 카테고리의 다른 글
| 아호 코라식(Aho-Corasick) 알고리즘(2) (0) | 2024.08.20 |
|---|---|
| 아호 코라식(Aho-Corasick) 알고리즘(1) (1) | 2024.08.14 |
| [백준 9663/Java] N-Queen (0) | 2023.05.07 |
| [백준 1874/Java] 스택 수열 (0) | 2023.03.18 |
| [백준 24267/Java] 알고리즘 수업 - 알고리즘 수행 시간 6 (0) | 2023.03.14 |

느리더라도 단단하게 성장하고자 합니다!
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!


![[백준 9663/Java] N-Queen](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FohiNN%2Fbtsd0nvLO9B%2FAAAAAAAAAAAAAAAAAAAAAHncYILNFjY09V9TEzCNH0q1-FBTS8L3ErCtkfVQQbXx%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DevgopWi%252F8TG3vaddXPzfjGVz7Mk%253D)
![[백준 1874/Java] 스택 수열](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FciPjkZ%2Fbtr4wMDN5fd%2FAAAAAAAAAAAAAAAAAAAAALjxWPeoM1Fa1SV09MUdUnNsBb4UMbJ16GEmcihqM5e5%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DcBjdzo4RJc0CokSmKVgVXsZodXY%253D)